SENA 2 Early Number Assessment

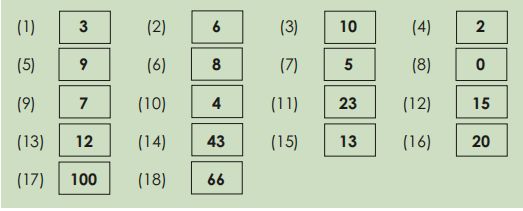
Numeral identification

Forward number word sequences

Start counting from … I’ll tell you when to stop.

What is the next number after …?

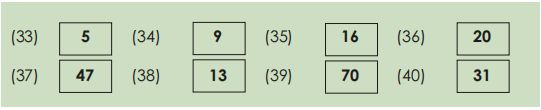
Backward number word sequences

Count backwards from … I’ll tell you when to stop What number comes before…?

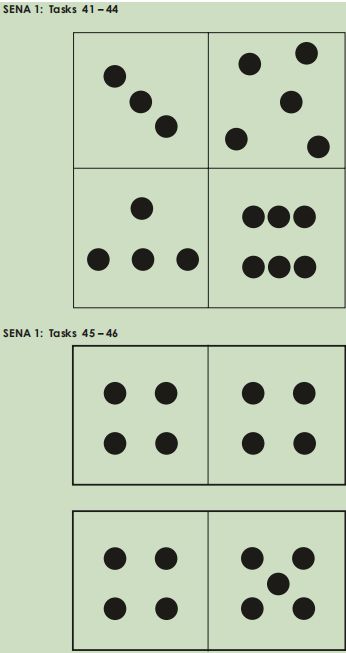
Subitising

How many dots are there?

Counting

Addition

Subtraction

Multiplication and division

Task(56)

Present a pile of counters, more than 12, to the student. (Randomly spaced, not in a line. Do not count them out.) Using these counters, make three groups with four in each group. How many counters are there altogether?

Interview guidelines

General

• Have an assessment sheet for each student being interviewed.

• Place the assessment sheet to the side of the work space and, if possible, out of the student’s view. (A small screen is useful for this purpose.)

• Note incorrect responses and any useful comments on the assessment sheet.

• Where useful, ask students how they solved the tasks.

• The interviewer should decide if it is necessary to give additional tasks or to abandon some of the set tasks.

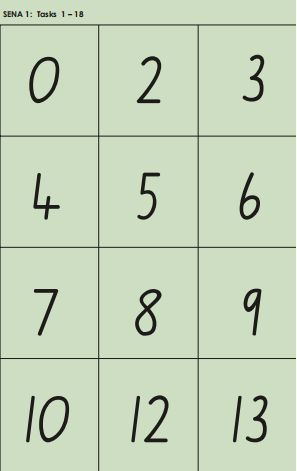
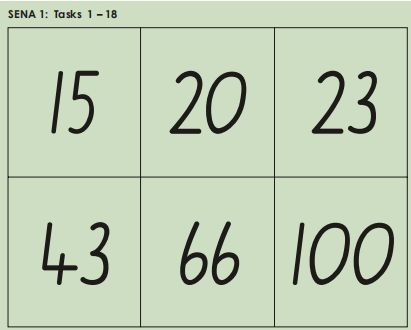
Numeral identification

(Tasks 1 – 18)

• Show the numeral cards in the order indicated.

Forward number word sequence (Tasks 19 – 29)

Tasks 19 – 21

• Stop if the student encounters difficulties.

Tasks 22 – 29

• For these “number after” tasks, the interviewer needs to decide if the student finds the “number after” by counting from one or can give the answer immediately.

• If necessary, give additional tasks (e.g. the number after 4, after 7, etc.)

Backward number word sequence (Tasks 30 – 40)

Tasks 30 – 32

• Don’t give Task 31 if the student has difficulty with Task 30.

Tasks 33 – 40

• For these “number before” tasks, the interviewer needs to decide if the student finds the “number before” by counting from one or can give the answer immediately.

Tasks 41 – 46

• Each of the domino patterns appears on a separate card.

• Display each card for approximately one second.

• If the student correctly identifies (45) and (46) ask, “How did you know there were… (9) dots?

Counting (Tasks 47 – 49)

Task 47

• Place the group of five blue counters in a random group (i.e. not in line or in the dice pattern of five).

• Don’t count the counters when placing them on the work space.

• When this task is completed, put the five counters to one side (to be used again in Task 49).

Task 48

• Place a collection of red counters (more than eight) on the work space.

Task 49

• If the student was successful with Tasks 47 and 48, place the eight red counters and the five counters in separate groups and ask: How many are there altogether?

• If the student was unsuccessful with Tasks 47 and 48, place 13 counters of the same colour in one group and ask: How many counters are there?

Addition (Tasks 50 – 52)

• Pay close attention to how the student solves these tasks.

• The interviewer is seeking to determine the student’s counting stage and will need to ask what the student did to achieve the answer.

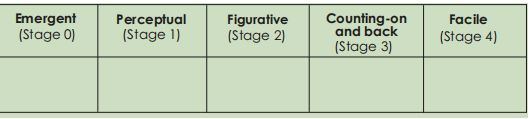
• Specifically, the interviewer is seeking to see if the student:

• can’t count visible items (stage 0 – emergent)

• can’t solve hidden tasks (stage 1 – perceptual)

• solves hidden task by counting from one (stage 2 – figurative)

• counts-on (stage 3 – counting-on-and-back)

• uses a more advanced strategy, e.g. making the ten and adding 3 (stage 4 – facile)

Subtraction (Tasks 53 – 55)

• Task 53 is verbal – no counters.

Tasks 54 – 55

• Present the counters as a group. Do not count them out in front of the student

• These tasks are designed to elicit at least figurative counting strategies.

Multiplication and division (Task 56)

Present more than 12 counters, randomly placed, to the student. The first instruction is designed to indicate if the student is able to form equal groups

Note how the student forms the groups. Does he or she drag the counters one at a time or many at a time to form a group? The follow-up question is intended to show the counting strategy which the student uses to find the total. A student using a less sophisticated strategy will count by ones, ignoring the structure of the groups. A more advanced strategy would be to use skip counting or repeated addition.

Numeral identification (Tasks 1 – 18)

Forward number word sequences (Tasks 19 – 29)

Backward number word sequences (Tasks 30 – 40)

Subitising (Tasks 40 – 46)

Early arithmetical strategies (Tasks 47 – 55)

Multiplication and division (Task 56)