MATH 221 Functions Assignment

Functions

3.1. Definition.

To specify a function f you must

1. give a rule which tells you how to compute the value f(x) of the function for a given real number x, and:
2. say for which real numbers x the rule may be applied.

The set of numbers for which a function is defined is called its domain. The set of all possible numbers f(x) as x runs over the domain is called the range of the function. The rule must be unambiguous: the same must always lead to the same f(x).

For instance, one can define a function f by putting f(x) = ?x for all x ? 0. Here the rule defining f is “take the square root of whatever number you’re given”, and the function f will accept all non negative real numbers.

The rule which specifies a function can come in many different forms. Most often it is a formula, as in the square root example of the previous paragraph. Sometimes you need a few formulas, as in g(x) = ( 2x for x < 0 xss=removed>

Functions which are defined by different formulas on different intervals are sometimes called piece wise defined functions.

3.2. Graphing a function.

You get the graph of a function f by drawing all points whose coordinates are (x, y) where x must be in the domain of f and y = f(x)

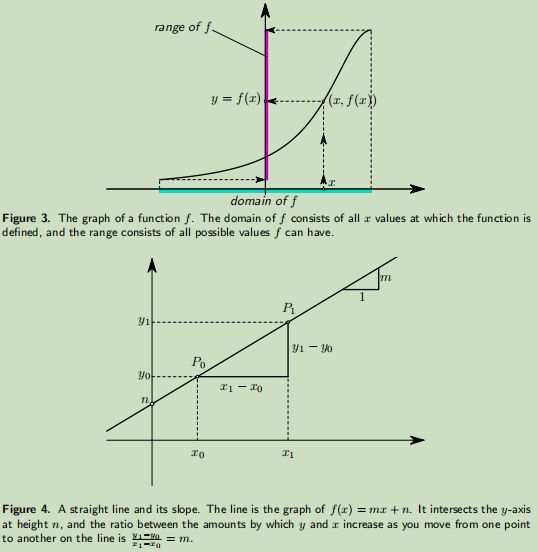
3.3. Linear functions.

A function which is given by the formula f(x) = mx + n where m and n are constants is called a linear function. Its graph is a straight line. The constants m and n are the slope and y-intercept of the line. Conversely, any straight line which is not vertical (i.e. not parallel to the y-axis) is the graph of a linear function. If you know two points (x0, y0) and (x1, y1) on the line, then then one can compute the slope m from the “rise-over-run” formula m = y1 ? y0 x1 ? x0 .

This formula actually contains a theorem from Euclidean geometry, namely it says that the ratio (y1 ? y0) : (x1 ? x0) is the same for every pair of points (x0, y0) and (x1, y1) that you could pick on the line.

3.4. Domain and “biggest possible domain. ”

In this course we will usually not be careful about specifying the domain of the function. When this happens the domain is understood to be the set of all x for which the rule which tells you how to compute f(x) is meaningful. For instance, if we say that h is the function h(x) = ?x then the domain of h is understood to be the set of all non negative real numbers domain of h = [0, ?) since ?x is well-defined for all x ? 0 and undefined for x < 0>

A systematic way of finding the domain and range of a function for which you are only given a formula is as follows:

• The domain of f consists of all x for which f(x) is well-defined (“makes sense”)
• The range of f consists of all y for which you can solve the equation f(x) = y.

3.5. Example – find the domain and range of f(x) = 1/x2.

The expression 1/x2 can be computed for all real numbers x except x = 0 since this leads to division by zero. Hence the domain of the function f(x) = 1/x2 is “all real numbers except 0” = x | x ^6 = 0= (??, 0) ? (0, ?).

To find the range we ask “for which y can we solve the equation y = f(x) for x,” i.e. we for which y can you solve y = 1/x2 for x?

If y = 1/x2 then we must have x2 = 1/y, so first of all, since we have to divide by y, y can’t be zero.

Furthermore, 1/y = x2 says that y must be positive. On the other hand, if y > 0 then y = 1/x2 has a solution (in fact two solutions), namely x = ±1/?y. This shows that the range of f is “all positive real numbers” = {x | x > 0} = (0, ?).

3.6. Functions in “real life. ”

One can describe the motion of an object using a function. If some object is moving along a straight line, then you can define the following function: Let x(t) be the distance from the object to a fixed marker on the line, at the time t. Here the domain of the function is the set of all times t for which we know the position of the object, and the rule is Given t, measure the distance between the object and the marker at time t.

There are many examples of this kind. For instance, a biologist could describe the growth of a cell by defining m(t) to be the mass of the cell at time t (measured since the birth of the cell). Here the domain is the interval [0, T], where T is the life time of the cell, and the rule that describes the function is Given t, weigh the cell at time t.

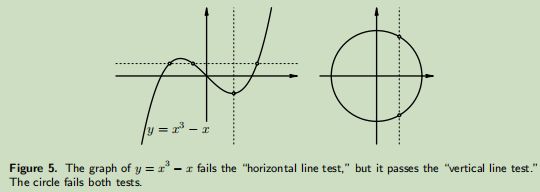
3.7. The Vertical Line Property.

Generally speaking graphs of functions are curves in the plane but they distinguish themselves from arbitrary curves by the way they intersect vertical lines: The graph of a function cannot intersect a vertical line “x = constant” in more than one point. The reason why this is true is very simple: if two points lie on a vertical line, then they have the same x coordinate, so if they also lie on the graph of a function f, then their y-coordinates must also be equal, namely f(x).

3.8. Examples

The graph of f(x) = x3 ? x “goes up and down,” and, even though it intersects several horizontal lines in more than one point, it intersects every vertical line in exactly one point.

The collection of points determined by the equation x2 + y2 = 1 is a circle. It is not the graph of a function since the vertical line x = 0 (the y-axis) intersects the graph in two points P1(0, 1) and P2(0, ?1).

Are you struggling to keep up with the demands of your academic journey? Don't worry, we've got your back! Exam Question Bank is your trusted partner in achieving academic excellence for all kind of technical and non-technical subjects.

Our comprehensive range of academic services is designed to cater to students at every level. Whether you're a high school student, a college undergraduate, or pursuing advanced studies, we have the expertise and resources to support you.

To connect with expert and ask your query click here Exam Question Bank