Data Mining and Neural Networks MA3022/MA4022

MA3022/MA4022/MA7022 Data Mining and Neural Networks

Homework 2

Due till 03.03.2025 100 marks available

Task 1. (20 marks) . Give the Bayes formula for two events and for multivalued random variables.

The probability a woman in the general population has breast cancer is 0.004. The probability that a positive mammography result occurs given that a woman has cancer is 0.40. (This is the sensitivity of the test.) The probability that a negative result will occur given that a woman does not have breast cancer is 0.95. (This is the specificity of the test.) Suppose a woman has a mammography exam and gets a positive result. What is the probability that she actually has breast cancer?

Task 2. (10 marks) Prove that k-means algorithm terminates after a finite number of steps. Construct an example of a dataset with the minimal number of data points for which the K- means algorithm (K=2) gives different clusters for different initial positions of centres.

Task 3. (20 marks) Describe the structure of Bayes net: what are vertices, directed edges between vertices, and what information do we keep with vertices? Give the definition of con- ditional independence. Compute the probabilitiesP(C&G) andP(B|F) from the given Bayes net (see figure ?? :

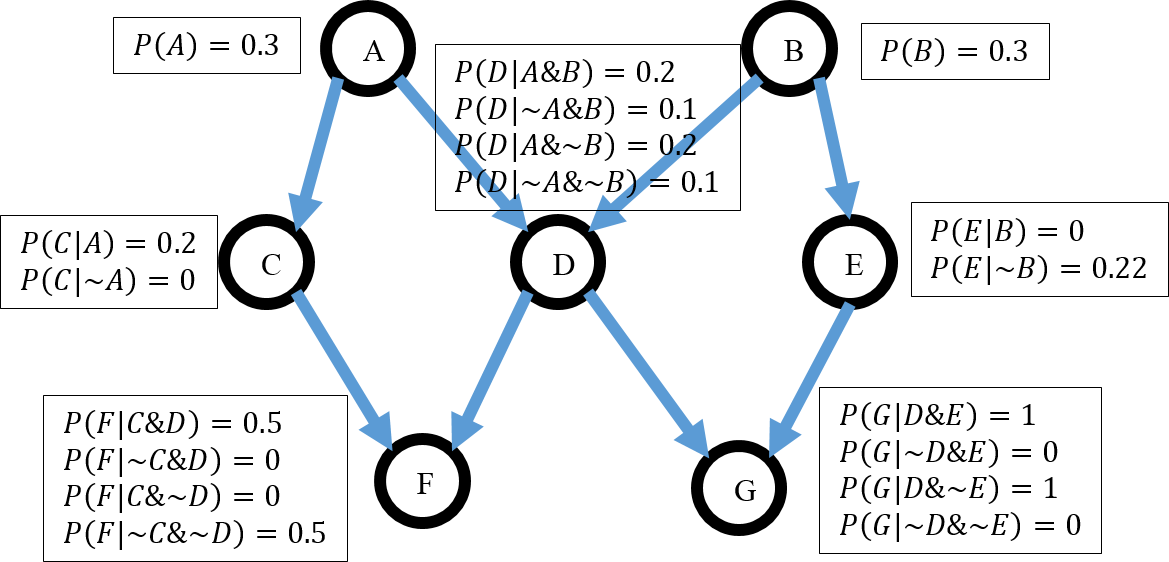
Task 4. (20 marks) Simpsons paradox. Consider a medical trial in which patient treatment and outcome are recovered. Two trials were conducted, one with 300 females and one with 300 males. The data are summarised in the table below. Does the drug cause increased recovery? According to the table for males, the answer is no, since more males recovered when they were not given the drug than when they were. Similarly, more females recovered when not given the drug than recovered when given the drug. The conclusion appears that the drug cannot be beneficial since it aids neither subpopulation. However, ignoring the gender information, and collating both the male and female data into one combined table, we find that more people re-covered when given the drug than when not. Should we recommend the drug? Create a Bayes net for this problem. How is it possible to avoid the paradox by sampling?

Females

Males

Combined

Task 5. (20 marks) Give the definitions of entropy, information gain and relative information gain. Calculate the entropiesH(C),H(C|A),H(C|B), information gain and relative information gainIG(C|A),RIG(C|A),IG(C|B), andRIG(C|B) for the following data table and create the decision tree for the target attribute C.

Task 6. (10 marks) Centralize data, find the covariance matrix and the principal components for the following dataset in 2D: