Informal Definition Of Limits Assignment

While it is easy to define precisely in a few words what a square root is (?a is the positive number whose square is a) the definition of the limit of a function runs over several terse lines, and most people dont find it very enlightening when they first see it. (See 2.) So we postpone this for a while and fine tune our intuition for another page.

1.1. Definition of limit (1st attempt).

limx=a: f(x) = L
is read the limit of f(x) as x approaches a is L. It means that if you choose values of x which are close but not equal to a, then f(x) will be close to the value L; moreover, f(x) gets closer and closer to L as x gets closer and closer to a. The following alternative notation is sometimes used
f(x) =L as x=a;
(read f(x) approaches L as x approaches a or f(x) goes to L is x goes to a.)

1.2. Example

If f(x) = x + 3 then
limx=4: f(x) = 7,
is true, because if you substitute numbers x close to 4 in f(x) = x + 3 the result will be close to 7.

1.3. Example: substituting numbers to guess a limit.

What (if anything) is
limx=2: x² ? 2x /x² ? 4 ?
Here f(x) = (x² ? 2x)/(x2 ? 4) and a = 2.

We first try to substitute x = 2, but this leads to
f(2) = 2²-2 2/ 2²-4 = 0/0
which does not exist. Next we try to substitute values of x close but not equal to 2. Table 1 suggests that f(x) approaches 0.5.

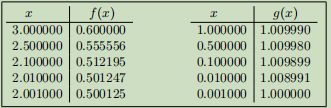
1.4. Example: Substituting numbers can suggest the wrong answer.

The previous example shows that our first definition of limit is not very precise, because it says x close to a, but how close is close enough? Suppose we had taken the function

g(x) = 101 000x /100 000x + 1
and we had asked for the limit limx=0 g(x).

Then substitution of some small values of x could lead us to believe that the limit is 1.000 . . .. Only when you substitute even smaller values do you find that the limit is 0 (zero)!

See also problem 29.

Are you struggling to keep up with the demands of your academic journey? Don't worry, we've got your back! Exam Question Bank is your trusted partner in achieving academic excellence for all kind of technical and non-technical subjects.

Our comprehensive range of academic services is designed to cater to students at every level. Whether you're a high school student, a college undergraduate, or pursuing advanced studies, we have the expertise and resources to support you.

To connect with expert and ask your query click here Exam Question Bank