Overview

This assessment seeks to analyze the overall displacement and the resultant forces in a truss-like structure based on the stiffness matrix using MATLAB. Part 1 deals with a structure comprising two members and with horizontal and vertical loads, whereas Part 3 generalizes the previously undertaken analysis by incorporating an inclined member. Hand calculations with the aid of the Moment-Area Method also confirm this finding. Both methods yield similar reliability indicating the validity of the MATLAB generated code. The performance of the students code is impressive; and the material stiffness transformation, the world stiffness matrices, and the boundary conditions are well managed in solving a variety of structural problems.

MATLAB code creation

MATLAB code creation in this assessment also obtained a very good understanding of the stiffness matrix method, structural transformations as well as boundary conditions for structural analysis problems.

Part 1

It consists of a two-bar system (AB and BC) to which horizontal and vertical loads are applied at point C. The geometry and material properties to be described are cross-sectional area to young Modulus ratio, moment of inertia, and lengths of the members. The stiffness matrices for each member are determined, and then converted to global stiffness matrices for the members, using a transformation matrix for elements that are at different angles to each other, with element AB at 0 and element BC at 90. Assembling of the global stiffness matrix is now done and boundary conditions are set (Point A is restrained while Point B and C are free to move). In this case, the code computes the displacements at point C and the reaction forces at point A.

Part 3

The calculations of a third member, C D, are added and set at 50 to the horizontal. A new stiffness matrix and transformation for the inclined member are added to the system. The new pinned boundary condition is correctly defined at point B and the program is capable of finding displacements at points C and D as well as the corresponding forces of reaction. In the modeling of beams, the implementation of the boundary conditions such as fixed and pinned supports is correct, and the use of the stiffness matrix method is employed well for calculating the structural responses throughout the code.

Calculation

Part 2

This part of the calculation process includes checking the released results by MATLAB code by the Moment-Area Method. In this method, displacements at point C and reaction forces at point A are computed. For horizontal and vertical reactions and the moment at the fixed support apply the principle of equilibrium.

Figure 1: Part 2 Calculation
(Source: Self)

The displacements obtained due to horizontal and vertical loads are in close agreement with the MATLAB results hence validating the numerical solution. The results from the hand calculations and MATLAB agree thus giving the engineer a reliable structural analysis.

Results and Discussion

Part 1

The analysis of the two-bar system provided values at point C and loads at point A. This obtained the global stiffness matrix and applied loads that characterize the structure under load.

Figure 2: Part 1 Output
(Source: MATLAB)

The analyses showed that certain displacements are indeed in concordance with the theoretical values predicted by theoretical structural mechanics, thus establishing the soundness of the stiffness matrix approach. The convergence between the MATLAB results and the theoretical values further confirms the effectiveness of the implemented code in simulating the primary response behaviors of the structure.

Part 3

The inclined member CD at 50 more complicated the system, however, the modified stiffness matrix can handle the addition.

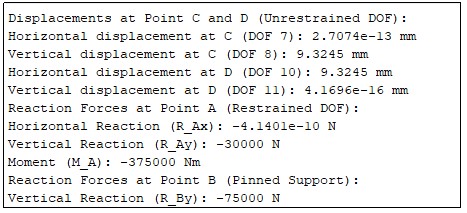
Figure 3: Part 3 Output
(Source: MATLAB)

The coordinate values entered in the program are correct the computations of new displacements at points C & D along with the associated reaction force are correct. The problem of pinned boundary conditions at point B is also correct and can solve support problems in a broad context. The Comparison of the results between MATLAB analysis. The hand-calculated results are found to tally with the MATLAB results, thus providing confidence in the methods used. The policies accentuate the significance of an empirical cross-check of computational methods by analytical procedures in order to obtain structurally sound figures. The findings confirm the applicability of the stiffness matrix method in analyzing complex truss systems in various loading conditions.

Conclusion

This assessment effectively showed how the stiffness matrix method can be employed to understand a truss-like structure in different loading scenarios. The values obtained from using the MATLAB code and the manual calculations are similar, indicating the accuracy of the numerical method. These scenarios are effectively managed in the analysis, and the additional inclusion of an inclined member is shown to be feasible using the method. The work is to improve the application of computational methods as a complement to traditional practices in structural engineering, demonstrating useful tools to engineers for analyzing complicated systems. It also increases insight while also generating accurate structural assessments that can be applied in real-life situations.

Are you struggling to keep up with the demands of your academic journey? Don't worry, we've got your back!
Exam Question Bank is your trusted partner in achieving academic excellence for all kind of technical and non-technical subjects. Our comprehensive range of academic services is designed to cater to students at every level. Whether you're a high school student, a college undergraduate, or pursuing advanced studies, we have the expertise and resources to support you.

To connect with expert and ask your query click here Exam Question Bank