Clustering, Classification, and Neural Networks in Data Science DSA4022

Question 1Clustering

b) Centroids:

Cluster 1: [2525378.03344482 153072.41471572]

Cluster 2: [862360.32335329 147073.61377246]

Cluster 3: [4127403.67847411 155618.71662125]

Interpretation:

KMeans clustering algorithm that we implemented found out three distinct clusters based on the dataset :

• Cluster 1: Represents households with moderate assets and relatively high annual income. This cluster might contain upper middle-class families with significant investments and steady, high-pay jobs

• Cluster 2 includes house holds with lower total assets but a fairly decent annual income. This segment might contain younger families or individuals who have not accumulated significant assets yet but still have good earning potential

• Cluster 3 comprises households with very high total asssets and a high annual income. This cluster likely includes wealthy families with extensive investments and a diverse source of incomes.

c) Since effective clustering depends on the right number of clusters, lets discuss some techniques to determine optimal number of clusters:

1.Elbow Method =>

1. This approach plots the within-cluster sum of squares (WCSS) against the number of clusters (K).
2. Main goal is to find the elbow point when the pace of decline decreases significantly, resulting in diminishing returns on sub-sequent clusters. This point indicates how many clusters is ideal
3. Elbow Method is a well-liked option for figuring out how many clusters there are in K-Means since it offers a visual depiction to help with K selection.

2.Silhouette scores =>

1. Measures an object's similarity to its own cluster in relation to other clusters
2. Greater values correspond to better-defined clusters; the range is -1 to 1.
3. The best option may be determined by calculating the silhouette score for various values of K and identifying the number of clusters with the highest average silhouette score.
4. Table of Dunn Index and Inertia for Different Values of K:

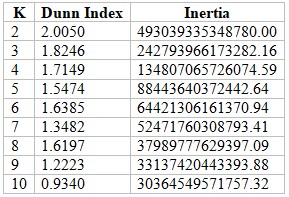
The value of K with the highest Dunn Index and lowest inertia is the optimal K.

Optimal K in terms of Dunn Index: K = 2 (Dunn Index = 2.0050)

Optimal K in terms of Inertia: K = 10 (Inertia = 30364549571757.32)

Question 2Weighted KNN

a) 1-Nearest Neighbour (1NN) is the simplest form, where a class label is determined solely by the closest neighbour. This method is highly sensitive to noise and outliers, which might lead to mis classification. Main advantage lies in its simplicity and ability to capture local data structures effectively.

K-Nearest Neighbours with takes care of some of the noise sensitivity by considering multiple neighbours, providing a more robust classification. However, its computationally expensive for large datasets and requires careful selection of the optimal.

n-Nearest Neighbours (nNN), where equals the training sample size, ensures all data points contribute, reducing variance. However, it might over-generalise by considering distant points equally, leading to poor performance and high computational costs.

Weighted Nearest Neighbor assigns high importance to closer neighbors, improving the classification accuracy. This method balances local and global data structures but require careful parameter tuning and is more computationally demanding than kNN.

b) Yes, the weighting factor aligns with intuition as closer points receive higher weights. An alternative is the Gaussian function:

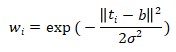
where sigma is the scaling parameter. This gives exponentially decreasing weights for points farther from the new data point.

Question 3Multi-layer NN

a) For this neural network, I chose a single hidden layer with 10 neurons and the ReLU activation function. ReLU is commonly used for hidden layers as it helps mitigate the vanishing gradient problem, which enables a model to learn faster and perform better. A single hidden layer with 10 neurons provide a good balance between model-complexity and computational efficiency, suitable for this binary classification task . The network was trained on the provided data set to identify at-risk students based on their GPA, attendance, duration of access to the LMS, and language test results.
The train accuracy was obtained as 61.8% and the Mean Squared Error was obtained as 0.382. This means that model performs fairly well and is able to correctly predict about 61.8% of the train labels.

b) To validate the implementation, the model was tested on the AtRiskStudentsTest.csv dataset. The accuracy and mean squared error (MSE) were chosen as the error functions.
Following are the obtained values for accuracy and MSE after testing:

• Test Accuracy: 0.534
• Test Mean Squared Error: 0.466

c) Table of Comparison:

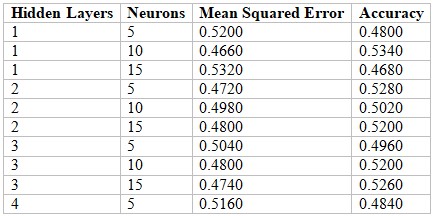
d) The process described in Part (c) help in determining the optimal number of hidden layers and neurons. In this case, the optimal combination is 1 hidden layer with 10 neurons.
However, this process has several drawbacks as discussed below:

• Training numerous models with varying configurations is computationally expensive and time-consuming. This approach may not be feasible for large datasets

• Choosing the number of hidden layers and neurons based solely on empirical results lacks theoretical guidance. This trial-and-error method does not provide insights into why certain configurations work better

• The optimal configuration found using this method may be highly dependent on the specific training and test datasets.

• The process may result in suboptimal performance if the tested configurations do not include the best possible setup.

Are you struggling to keep up with the demands of your academic journey? Don't worry, we've got your back!
Exam Question Bank is your trusted partner in achieving academic excellence for all kind of technical and non-technical subjects. Our comprehensive range of academic services is designed to cater to students at every level. Whether you're a high school student, a college undergraduate, or pursuing advanced studies, we have the expertise and resources to support you.

To connect with expert and ask your query click here Exam Question Bank