Statistical Computing Assignment

Assessment 5

General Instructions:

Make a copy of the Rmarkdown template and name it in this format: LastNameFirstName- Hw6.Rmd, and put it in your R working directory. You will submit a pdf generated from this Rmd file. Your knitted pdf file should show the code for the function, and, if asked, the results from running it.

Your submission should contain only the edited version of your final work, and not be a dump of all the work you did. Hence you should edit your assignment so that it is as concise as possible. Include only what is necessary for supporting your answers. Points will be deducted for handing in unnecessary code or for not editing your output.

If you use any material, e.g. books, papers, websites, that helped with your submission, they should be referenced and acknowledged. Such material should only be used to inform your work. If it is found that your work is very similar to work found on the internet, or other resource, you will get a zero. If students work are essentially the same, points scored will be divided by the number of students involved.

where ? is the standard normal CDF.

Write code that would allow you to perform a simulation study to examine this property, i.e. you want to simulate data, compute and plot the empirical CDF and also draw the standard normal CDF ?(x). In other words, for your plot, the x-axis are values of x, and the y-axis is P (Z_n ? x) (which you compute using your simulated Z_ns), and the theoretical ?(x).

You should write a brief paragraph or two to describe your simulation study and what your code does. Run your code for a specific example, and explain your output.

2. In 1693 Samuel Pepys and Isaac Newton corresponded over a problem posed by Pepys in relation to a wager he planned to The problem was:

Which of the following three propositions has the greatest chance of success?

• Six fair dice are tossed independently and at least one 6
• Twelve fair dice are tossed independently and at least two 6s

• Eighteen fair dice are tossed independently and at least three 6s

One can solve this using binomial probabilities, but for this question, you will use simulation in R to figure out the answer. That is, write a function to simulate tossing six fair die, and use it to estimate the probability for (a). Then write functions to estimate the probabilities for (b) and (c). What does your simulation say about your answer to the problem posed by Pepys?

There are two formulas to approximate the variance of ?^(h), based on different assumptions:

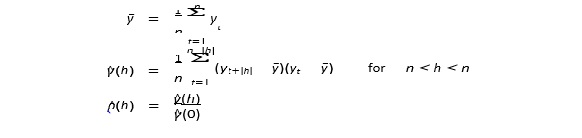
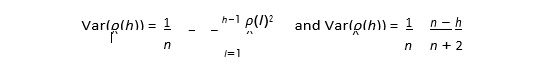
Do a simulation study to explore how accurate these two approximation formulas are for the AR(1) model, for h = 1, 5 and 10. Remember to write modular code - write functions to do specific tasks and then put these functions together.

To simulate the time series, set y_t = 0 for t = ?20 as the starting value, and keep only the observations y₁, y₂, . . . y_n.

Note that you need to choose values for the parameters in order to generate the data. You can set ? to be 0 and not consider that particular parameter in your simulation.